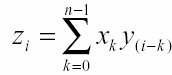
| цкюбмюъ | днйкюдш | наясфдемхе | |
Модели памяти, основанные на математической операции свертки (
Convolution-based memory models)[1].Общая идея
CBMM (Convolution-based memory models) - это класс математических моделей, основанных на представлении о распределенном хранении данных в нервной системе. Все модели данного типа используют операцию свертки в схемах формирования энграммы (отпечатка в памяти).
Запоминаемая информация обычно представляется в виде бинарного или цифрового вектора (pattern) и сохраняется в виде множества взаимосвязей этих векторов.
Свойства и математическое описание моделей очень похожи на свойства и математическое описание световой голограммы, поэтому они иногда называются голографическими моделями памяти
. Например, так же как и в голограмме, в модели возможна реконструкция (хотя и в зашумленном виде) данных по зашумленному образцу или только по части образца, что является следствием распределенного хранения информации.Процесс формирования энграммы
описывается двумя операциями: суперпозицией и связыванием (ассоциированием). Для образцов в виде числового вектора суперпозицией является обычная операция сложения. В качестве операции связывания (ассоциирования) используется свертка. Для n мерных векторов она равна: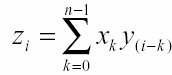
Обычно используется сокращенная запись этого уравнения
:![]()
В моделях могут использоваться различные варианты расчета свертки. Например
, "кольцевая" свертка, которая может быть представлена как "компрессия" векторного произведения, полученная суммированием соответствующих элементов (см. след. рис.)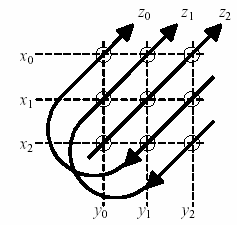
Результатом кольцевой свертки является вектор той же размерности
n, что и исходные векторы X, Y.Важным свойством свертки является сохранение подобия
. Например, если red подобно pink то redдsquare подобно pinkдsquare в той же степени. Степень подобия может быть выражена численно, по формуле: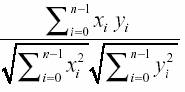
Свертка легко может быть декодирована с помощью обратной операции свертки
:red
-1дredдcircle = circle.При этом используются методы приближенного вычисление, так как точная операция численно нестабильна при наличии шума
.Таким же способом возможно декодирование суперпозиции нескольких ассоциаций. Например, суперпозиция
(redдcircle)+(blueдsquare) может быть декодирована так:Blue-1
д ((red дcircle)+(blueдsquare))= (blue-1д redдcircle) + (blue-1д blueдsquare)╩ square.(
blue-1д red д circle) - не будет подобно ни одному из элементов blue, red, circle, square и может рассматриваться как шум, а значение (blue-1д blueдsquare) равно зашумленной версии square.При многократной суперпозиции
увеличивается зашумление данных (эффект интерференции). Увеличение размерности вектора, представляющего данные, снижает степень зашумленности при декодировании.Модель
TODAM (Theory of Distributed Associative Memory) [2]Модель создана для описания экспериментальных результатов, полученных в опытах по исследованию запоминания человеком списка ассоциативных пар слов. Эксперименты обычно проводят следующим образом. Испытуемого просят запомнить список пар слов, например
: "корова-лошадь, собака-кошка, ручка-карандаш". Затем ему задают вопросы такого типа: "Было ли в списке слово "машина"?" (тест на распознавание), "Какое слово было в паре со словом "кошка"?" (тест на вспоминание по ассоциации). В экспериментах варьируются такие параметры как: длина списка, степень известности слов, степень их подобия (однородность) и положение слов в списке. Данные о количестве и типе ошибок, возникающих при ответах, позволяет изучить и понять некоторые свойства человеческой памяти.Модель формирования энграммы в модели
TODAM описывается формулой:T
j= a T j-1+g1 x j+g2 y j +g3 x j дy jГде
Tj √ вектор, представляющий энграмму списка из j ассоциативных пар.a
, g1, g2, g3 √константы модели, имеющие значение в диапазоне от 0 до 1.Xj, Yj √ векторы, отображающие ассоциированную пару слов из списка.
В численных экспериментах считается, что образец распознаваем по энграмме, если скалярное произведение энграммы и образца больше некоторого порога шума. Образец X из пары (X,Y) считается вспомненным ассоциативно, если операция x-1дT √ позволяет реконструировать значение y.
Модель
TODAM позволяет воспроизводить следующие известные в психологии (полученные экспериментально) закономерности: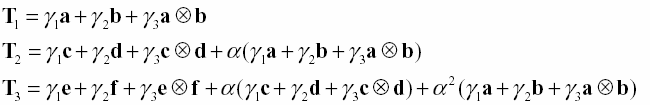
Отсюда видно, что забывание слов пропорционально
aj-1.Следует заметить, что в реальных экспериментах обнаруживается также и эффект первенства (
primacy effect) √ слова из начала списка запоминаются лучше чем из середины. Но данная модель не описывает этот эффект (для его воспроизведения необходима модель, включающая описание взаимодействия кратковременной и долговременной памяти).Модель
CHARM ("Composite Holographic Associative Recall Model") [3]Модель ориентирована на описание эффекта однородности списка запоминаемых ассоциативных пар. Формирование энграммы описывается формулой
:T
i = Еx i дy i.Т.е. это сокращенная версия
TODAM, в которой сохраняется только ассоциативная информация.Одним из эффектов, воспроизводимой моделью, является снижение способности к запоминанию списков с похожими образцами. В реальных экспериментах это проявляется,
например, в том, что список, состоящий только из известных имен, запоминается хуже, чем список, состоящий из слов на совершенно разные темы. Более того, в модели, как и в реальных экспериментах, наиболее часто наблюдался один и тот же тип ошибки √ ошибочное вспоминание по ассоциации слова, имеющегося в списке и похожего на требуемое.Модель HRR
s (Holographic Reduced Representations)[4]Это модель, способная оперировать рекурсивной информационной структурой. Она необходима для решения таких когнитивных задач, как, например пониманием естественного языка.
В
HRRs модели энграмма фразы "политики говорят неправду" выглядит так:ЭНГговорят
=ПОЛИТИКИ+ГОВОРЯТ+НЕПРАВДУ++ГОВОРЯТконтейнердПОЛИТИКИ+ ГОВОРЯТсодержимоедНЕПРАВДУ
В формуле большими буквами обозначены векторы, представляющие слова из фразы, мелким курсивом √структура с точки зрения которой рассматривается слово.
Если нам известна энграмма ЭНГговорят
и значение контейнера ГОВОРЯТконтейнер, то мы можем "вытянуть" содержимое контейнераГОВОРЯТ
-1контейнердЭНГговорят ╩ ПОЛИТИКИЭнграмма
ЭНТговорят является редуцированным представлением фразы ⌠политики говорят неправду■, которая также может выступать в роле содержимого для контейнера более высокого порядка. Например, фраза ⌠я думаю, политики говорят неправду■ может быть представлена так:ЭНГ
думаю=Я+ДУМАЮ+ЭНГговорят+ ДУМАЮконтейнердЯ++
ДУМАЮсодержимоедЭНГговорятЭнграмма более высокого уровня ЭНГдумаю может быть декодирована:
ДУМАЮ
-1контейнердЭНГдумаю ╩ ЭНГговорятCBMM
модели в нейронных сетяхМатематические операции, используемые в
CBMM моделях, могут быть воспроизведены в "sigma-pi" нейронных сетях. Например, так будет выглядеть нейронная сеть, вычисляющая кольцевую свертку двух векторов: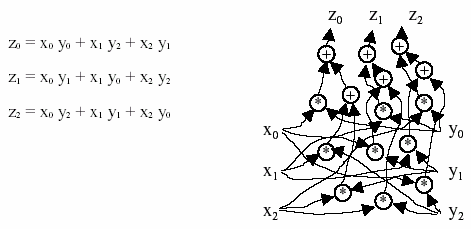
Может показаться, что реализация таких операций слишком сложна и требует слишком большой точности организации для биологических систем. Однако, в работах
[5, 6] было показано, что "sigma-pi" нейронная сеть, осуществляющая суммирование произведений случайно выбранных элементов двух векторов, может выполнять операции кодирования и декодирования. Причем эти операции обладают теми же свойствами, что и операции свертки.Литература
| цкюбмюъ | днйкюдш | наясфдемхе | |